What is the size(magnitude) of the subsequent vector of cross item ?

It is the territory of the zone surrounde by the two vectors.Following is the idea of Cross Product spoke to in numerical recipe. The figuring appeared in condition (2) may look pretty basic, however on the off chance that the vector goes into higher dimesion the estimation goes dramatically muddled. In any case, as I stated, don't stress over this. Programming would do it for you vector cross product calculator.

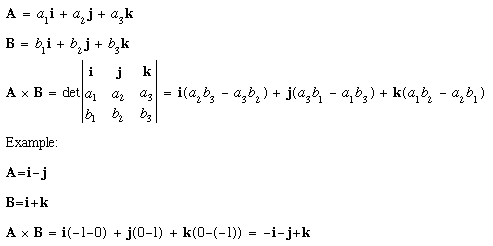
If you think about the significance of the condition and representation appeared above, if both the vector u and v are on x-y plane, the subsequent cross item vector is consistently in corresponding with z pivot. Since the vector u and v is on x-y plan, you can speak to these two vector as a three dimensional vector as as follows. (Why we have to make these vector as a three dimensional structure ? It is on demonstrated the grounds that the cross result of the two vectors need at any rate three dimensional space. It is on the grounds that the subsequent vector from cross item is opposite to the vectors given for the cross item. That is, the subsequent vector of "u x v" is opposite to v and u. Despite the fact that you can speak to u and v in 2 D plan, you need 3D space to speak to u and v and 'cross item' all together.

You may believe that I am purposefully muddle a basic thing. From the start look, it would glance excessively convoluted as far as count however this one has a preferred position. In the event that you need to ascertain the cross item utilizing the condition toward the start of this page, you have to sort out point between the two vectors. Notwithstanding, sorting out the points between the two vectors isn't simple (you would need to do Inner Product of the two vectors to sort out the point between the two vectors). In any case, in the event that you use ascertain the cross item thusly (i.e, utilizing the determinant), you don't need to stress over sorting out the point between the two vectors.

The cross item is a numerical activity that can be performed on any two, three dimensional vectors. The aftereffect of the cross item activity will be a third vector that is opposite to both of the first vectors and has a size of the principal vector times the size of the subsequent vector times the sine of the point between the vectors.

When finding a cross item you may see that there are really two bearings that are opposite to both of your unique vectors. These two bearings will be in precise inverse ways. To discover which of these two headings the cross item utilizes, we will utilize the correct hand rule.

To utilize the correct hand rule, hold out you right hand, point your pointer toward the principal vector, turn your center finger in towards the course of the subsequent vector, and hold your thumb up. Your thumb should now point toward the cross item vector.